Ciberacertijos
Acertijos gráficos para ejercitar la lógica y el pensamiento lateral.
27/11/12
 Se nota que no tuve muchas ganas de escribir estos días, pero no dejaré que el mes se escape sin hacer algo por tu cerebro, aunque la mayor parte del trabajo la tendrás que hacer por tu cuenta: pensar y resolver ocho acertijos gráficos, algunos muy fáciles, que requieren habilidades lógicas elementales, y otros que exigen un poco de pensamiento lateral o simplemente mucha paciencia.
Se nota que no tuve muchas ganas de escribir estos días, pero no dejaré que el mes se escape sin hacer algo por tu cerebro, aunque la mayor parte del trabajo la tendrás que hacer por tu cuenta: pensar y resolver ocho acertijos gráficos, algunos muy fáciles, que requieren habilidades lógicas elementales, y otros que exigen un poco de pensamiento lateral o simplemente mucha paciencia.Afirmaciones

Todas las personas se contradicen unas a otras, así que sólo una puede decir la verdad. Eso significa que nueve mienten, por lo tanto, la persona 9 dice la verdad.
Batalla estelar

 La nave debe ubicarse en E8.
La nave debe ubicarse en E8.Los rayos resultantes serán:
- E8 a A7
- E8 a A2 (pasa por C5)
- E8 a E3 (pasa por E4)
- E8 a G2 (pasa por F5)
- E8 a H5 (pasa por F7)
Pensatiempo

El número en cuestión no es visible y hay que deducirlo: si se observa la posición de las manecillas, se notará que están perfectamente distribuidas, dividiendo la circunferencia del reloj en tres partes iguales. Dado que el círculo tiene 360º, la respuesta es 120.
Pixelado
Laberinto
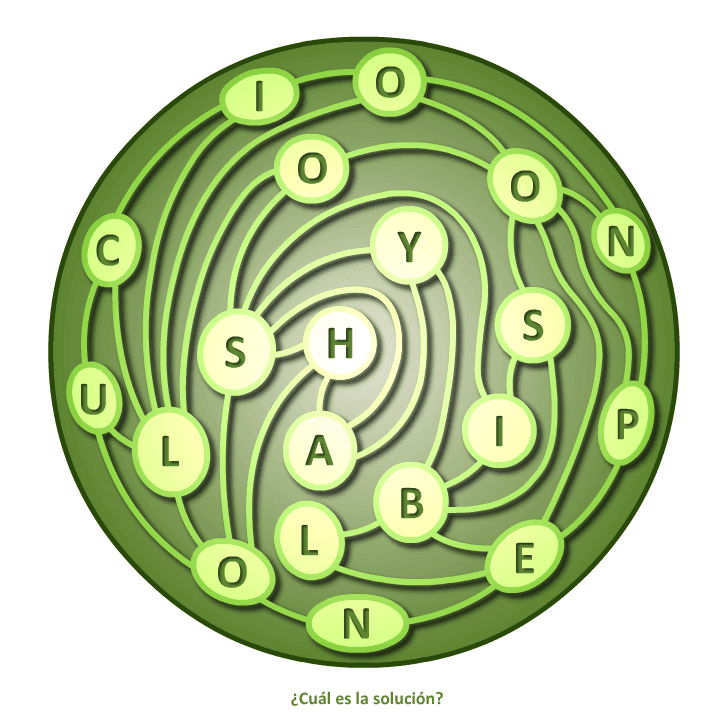
No hay solución posible, literalmente.


Pirámide numérica

El número central debe ser 3, siguiendo esta lógica aritmética: desde abajo hacia arriba, se resta cada par de números contiguos y se pone el resultado sobre ellos, por ejemplo: 20 - 10 = 10, 10 - 7 = 3, 7 - 5 = 2, etcétera.
Nosotras

La respuesta es letras: "dos por tres" contiene 10 letras, "tres" tiene 4 letras, "cinco más dos" suman 11 letras y "aunque once" son apenas diez.
Mentiras

Supongamos que 3 dice la verdad. En ese caso, 1 y 2 mienten. Esto concuerda con la afirmación de 2 (que estaría mintiendo y dándole la razón a 3), pero no con la de 1: si 1 mintiera, 2 diría la verdad, pero no puede porque 3 dice que miente. Esta contradicción no permite que 3 diga la verdad. Por lo tanto, sabemos que 3 miente. Ahora supongamos que 2 dice la verdad, es decir, que 3 miente, lo cual ya hemos determinado que es verdad. Así que 2 debe decir la verdad. Y como 1 dice que 2 miente, 1 debe estar mintiendo porque acabamos de ver que 2 dice la verdad. Concluimos que: 1 miente, 2 dice la verdad y 3 miente.
Un error común sería pensar que, si 3 miente, 1 y 2 deben decir la verdad, pero eso no es lógico. Si 3 miente, sólo implica que su afirmación es falsa, lo cual puede significar que ni 1 ni 2 mienten, que miente únicamente 1 o que miente sólo 2. La segunda opción nos permite resolver el problema.
Un error común sería pensar que, si 3 miente, 1 y 2 deben decir la verdad, pero eso no es lógico. Si 3 miente, sólo implica que su afirmación es falsa, lo cual puede significar que ni 1 ni 2 mienten, que miente únicamente 1 o que miente sólo 2. La segunda opción nos permite resolver el problema.



Me gusta el detalle de las respuestas, al fin puedo dormir en paz.
ResponderEliminarSe agradecen las respuestas!!
ResponderEliminarNotable!! Me divertí un buen rato!! Y sí, las respuestas están al clavo!
ResponderEliminarEl primero bien hecho :D. Ya empezando el segundo, pero no entiendo como viajan los rayos.. van para cualquier lado? como va de A1 a E6?
ResponderEliminarya entendí, viajan recto siempre y si se cruzan otra nave la rompen ja
ResponderEliminarcheck 2, basta hasta que termine! :P
ResponderEliminarMuy bueno ayeronauta, de todas formas no acerté ninguna, pero igualmente muy bueno.
ResponderEliminarRealmente muy buenos, tengo poco tiempo visitando tu página y esta la primera vez que comento. Muy divertidos, tuve pretexto para no trabajar jajaja.
ResponderEliminarSolamente el acertijo del laberinto no lo resolví completamente (sin querer dar pistas de la respuesta) no sabía que tenía que ser toda ella...
Qué bueno que se hayan divertido. Otro día haré más :)
ResponderEliminarAcerté 3, por que no tenia ganas de resolver los demás, con un poco mas de tiempo tal vez lo conseguía.
ResponderEliminarhey, lo mismo que howlingWolf.. y eso que lo había leído antes :P.. jaja. buenos!
ResponderEliminarMuy bueno, x suerte tenia respuestas.. Solo acerte la 1 je. Ayreo... Has leído el libro sex code? Creo q ahí habría su diente material para q porongueti tuviera su propio espacio en el blog ja. Hace tiempo q no se aparece y se lo extraña. Saludos!
ResponderEliminarSuficiente* tengo auto completar y me cambia todo lo q escribo u.u
ResponderEliminarPude hacer la mayoría, gran trabajo ayreo :).
ResponderEliminarExcelente todo tu blog no me canso de leerlo y recomendarlo, y apenas hace 24 horas que me lo encontré buscando recetas para el fin del mundo!!! jajaja
ResponderEliminarSuerte con todo!
Es lógico. Según estudios de la Universidad de Internet, el tiempo promedio de cansancio es de 25 horas.
ResponderEliminarYo no pude resolver ninguna... ¿significa que debo ir al colegio de nuevo o que estoy tres escalones mas abajo en la escalera evolutiva?
ResponderEliminarPense que habia resuelto el "pensatiempo", ya que el numro romano II se repite tres veces, pero despues al ver la respueste, llore toda la tarde y me di de cabeza contra la pared...
Quizás fue un problema de mala administración del tiempo; no hacía falta pensar mucho sino largo. La mayoría de estos acertijos puede resolverse mediante prueba y error. Y si te sirve de consuelo aunque no pueda reparar los daños a tu pared: me diste una idea para un post...
ResponderEliminar5 de 8, nada mal
ResponderEliminarvamoosss q acerte los 9!!!
ResponderEliminarSon ocho...
ResponderEliminarEl de la nave espacial está muy divertido , por un momento me imaginé ahí
Eliminar